(تصاویر) بیوگرافی ارشمیدس؛ بزرگترین دانشمند دوران باستان

ارشمیدس شاید قدیمیترین دانشمندی باشد که جزئیاتی از زندگیاش دردسترس مانده است. او در زمینههای علمی مختلفی تأثیرگذار بوده است.
ارشمیدس (Archimedes)، ریاضیدان، فیزیکدان، مهندس، مخترع و منجم یونانی بود که در قرن سوم پیش از میلاد میزیست. اگرچه جزئیات زیادی از زندگی او در دست نیست، اکثر تاریخنگاران او را بزرگترین دانشمند دوران باستان میدانند.
به گزارش زومیت، ارشمیدس مفاهیم مدرن دیفرانسیل و ریاضیات تحلیلی را بنا کرد. بهعلاوه، با استفاده از روشهای نوین ریاضی، در ارائهی نظریهها و اثباتهای مهم هندسی هم نقش ایفا کرد. مساحت دایره و مساحت و حجم کره و مساحت زیرسهمی، از مواردی بودند که ارشمیدس محاسبه کرد.
از دیگر دستاوردهای مهم ارشمیدس در تاریخ ریاضیات، میتوان به محاسبهی حدودی عدد پی، محاسبهی مارپیچ ارشمیدس، ابداع روشی نمایی برای نشاندادن اعداد بسیار بزرگ و موارد مشابه اشاره کرد. بهعلاوه، او اولین فردی بود که مفاهیم ریاضی را در فیزیک بهکار برد و مفاهیمی همچون هیدرواستاتیک و استاتیک را تحلیل کرد. این دانشمند بزرگ محاسبات بنیادی اهرم را نیز انجام داد.
همانطورکه گفته شد، ارشمیدس علاوهبر ریاضی و فیزیک، دستی هم بر مهندسی و اختراع داشت. او افتخار طراحی چند ماشین نوآورانه ازجمله پمپهای پیچی (مبتنی بر مارپیچ ارشمیدس) و قرقرههای ترکیبی و بسیاری تجهیزات دفاعی را نیز دارد. ماشینهای او در نبردها برای دفاع از محل تولدش، یعنی سیراکوزا، استفاده میشدند.
ارشمیدس با وجود دستاوردها و یافتههای باارزش علمی، در دوران خود آنچنان شناختهشده نبود. یافتههای علمی او، سالها بعد و در میانهی قرن اول میلادی، بیشتر مطالعه و بررسی شدند و دانشمندان مختلف با بهرهگیری از آنها، مفاهیم ریاضیات و فیزیک را توسعه دادند. بههرحال، امروز ارشمیدس پایهگذار بسیاری از مفاهیم علمی شناخته میشود و نامش بهعنوان یکی از پیشگامان علوم پایه میدرخشد.
 پرترهی داستان مرگ ارشمیدس
پرترهی داستان مرگ ارشمیدس
تولد و شخصیت علمی
قطعا اطلاعاتی که دربارهی ارشمیدس و کودکی او وجود دارد، کلیاتی بیش نیستند و نمیتوان تاریخهای دقیقی دربارهاش ذکر کرد. البته دربارهی زندگی او، اطلاعاتی بیش از دانشمندان دیگر دوران باستان وجود دارد؛ اما بخشی از آنها تنها حکایت هستند و اسناد تاریخی دقیقی برایشان موجود نیست.
طبق اکثر اسناد موجود، ارشمیدس در سال ۲۸۷قم و در شهر سیراکوزا در جزیرهی سیسیل متولد شد. پدر ارشمیدس ریاضیدان و ستارهشناسی بهنام فیدیاس بود. خود ارشمیدس در کتابش با نام The Sand Reckoner، به ستارهشناسبودن پدرش اشاره میکند و میگوید پدرش بهدنبال محسابهی حدودی ابعاد خورشید بود. ارشمیدس در کتابش مینویسد:
بهجز اینها، جزئیات بیشتری از زندگی او در دست نیست و تنها تصور میشود خانوادهی ارشمیدس از اشرافزادگان سیراکوزا بودند. آنها احتمالا ارتباطاتی با پادشاه آن زمان منطقه، یعنی هیرو دوم نیز داشتند.
ارشمیدس در خانوادهای اشرافی و از نزدیکان پادشاه سیراکوزا متولد شد
در قرن سوم پیش از میلاد، سیراکوزا مرکزی برای تجارت و هنر و علم شناخته میشد. ارشمیدس از موقعیتش بهعنوان شهروندی در آن منطقه برای ارضای کنجکاویها و پرداخت به علاقهی همیشگیاش، یعنی حل مسئله استفاده کرد.
او پس از کسب آموزشهای اولیه از استادانش در سیراکوزا، به مصر سفر کرد تا در اسکندریه، مطالعات و تحصیل خود را ادامه دهد. اسکندریه را که در سال ۳۳۱قم اسکندر مقدونی تأسیس کرده بود، در آن سالها اعتبار زیادی بهعنوان مرکزی برای تحصیل و تحقیق کسب کرده بود.
اقلیدس، یکی از دانشمندان مشهوری بود که پیش از ورود ارشمیدس، در اسکندریه حضور داشت. او ستارهشناسی بزرگ بود و همچنین، دستاوردهایی نیز در علم هندسه داشت. یافتههای اقلیدس بعدها در تحقیقات علمی و دستاوردهای ارشمیدس نقش حیاتی داشتند.
ارشمیدس پس از تحصیل در اسکندریه، به سیراکوزا بازگشت و زندگی خود را برپایهی تفکر و اختراع پیش گرفت. از افسانههای مشهوری که دربارهی بازگشت ارشمیدس به سیراکوزا وجود دارد، ارتباط نزدیک او با پادشاه آن زمان، یعنی هیرو دوم بود و گفته میشد ارشمیدس تلاش زیادی میکرد تا مسائل درگیرکنندهی ذهن پادشاه را حل کند.
 کتاب گمشدهی ارشمیدس که در قرن بیستم کشف شد
کتاب گمشدهی ارشمیدس که در قرن بیستم کشف شد
برخی از آثار بهجامانده از ارشمیدس در نامههایی یافت میشوند که او از سیراکوزا به دوستش اراتوستن مینوشت. در آن زمان، ارتوستن مدیر کتابخانهی اسکندریه و دانشمندی بزرگ بود. او اولین فردی بود که اولینبار ابعاد سیارهی زمین را بهدرستی محاسبه کرد.
همانطورکه گفته شد، یافتهها دربارهی زندگی ارشمیدس بیشتر از دانشمندان باستانی دیگر است. البته، اکثر آنها حکایتهایی هستند که به تأثیرات او بر علومی همچون ریاضیات و فیزیک میپردازند.
بههرحال، پرداختن به همان یافتهها و داستانهای احتمالی مرتبط با آنها، زمینهی اکثر نوشتههای بیوگرافی دربارهی ارشمیدس است. ارشمیدس در فرهنگ علمی یونان باستان غرق بود که درنهایت، او را به یکی از ذهنهای باارزش تاریخ بدل کرد. برخی او را انیشتین زمان خود میدانند؛ درحالیکه بهتر است انیشتین را ارشمیدس زمانهی خود بدانیم.
نکتهی مهم دربارهی ارشمیدس آن است که دانشمندان دوران رنسانس در قرن شانزدهم باردیگر دستاوردهای او را بررسی کردند. آنها میدانستند ارشمیدس در یافتههای علمی خود درست عمل کرده است؛ اما این سؤال را از خود میکردند که چگونه در آن زمان، این دستاوردها حاصل شدهاند.
در طول تاریخ، ارشمیدس دانشمندی با رفتارهای خاص نیز شناخته میشود. او اثباتهایی بر یافتههای خود ارائه میکرد؛ اما روشهای خود را کامل شرح نمیداد. درواقع، او به اذیتکردن و دستانداختن ریاضیدانان دیگر نیز علاقه داشت. در داستانهایی گفته میشود پاسخ صحیح مسئلهها را به ریاضیدانان میداد و منتظر بود تا آنان روش حل مسئله را خودشان کشف کنند.
 پرترهای از اراتوستن (البته استفاده از کتاب به این شکل در آن زمان قطعا مرسوم نبوده است)
پرترهای از اراتوستن (البته استفاده از کتاب به این شکل در آن زمان قطعا مرسوم نبوده است)
کتاب گمشده
داستان نهفته در ریاضیات ارشمیدسی تا قرن بیستم ناشناخته مانده بود. در سال ۱۹۰۶، پروفسور یوهان هایبرگ کتابی در شهر قسطنطیه (استانبول امروزی) پیدا کرد. کتاب کشفشده نوعی کتاب دعای مسیحی نوشتهشده در قرن سیزدهم میلادی بود.
در آن زمان، قسطنطیه بهعنوان آخرین پایگاه امپراتوری روم شناخته میشد. در دیوارهای آن شهر، بسیاری از کتابها و مقالههای نوشتهشده در دوران یونان باستان مخفی شده بودند. کتابی که هایبرگ پیدا کرد، بهنام Archimedes Palimpsest شناخته میشود.
نکتهی جالب دربارهی کتاب گمشدهی ارشمیدس آن است که دعاهای مسیحی موجود در آن، روی نوشتههای علمی ریاضیاتی نوشته شدهاند. درواقع، راهبان تلاش کرده بودند متون اصلی را پاک و از آن بهعنوان کاغذی برای کتاب دعا استفاده کنند.
درنهایت، آثاری کمرنگ از تحقیقات ارشمیدس در کاغذها باقی مانده بود. درنهایت، باستانشناسان به این نتیجه رسیدند که آن کتاب بازسازی تحقیقات ارشمیدس بوده که در قرن دهم میلادی نوشته شده بود.
بسیاری از یافتههای ارشمیدس تا قرنها بعد ناشناس ماندند
کتابی که در قرن بیستم کشف شد، شامل ۷ رساله از مقالههای ارشمیدس بود. یکی از رسالههای مهم با نام The Method شناخته میشود که قرنها ناپدید شده بود. در آن کتاب، ارشمیدس روشهای تحقیقاتی خود در ریاضی را توضیح داده بود. او رسالهاش را به اراتوستن فرستاده بود تا در کتابخانهی اسکندریه نگهداری شود. او دربارهی رسالهاش گفته بود:
ریاضیدانان قرن بیستم با مطالعهی همان رسالهی ارشمیدس به این حقیقت پی بردند که او چقدر از زمانهی خود جلوتر بود و روشهایش برای حل مسائل چقدر خاص بودند. بهعنوان مثال، او توانسته بود سریها را محاسبه و از کشفیات خود در فیزیک و برای درک مواردی همچون نحوهی کار اهرمها استفاده کند. حتی در محاسبهی مرکز ثقل نیز ارشمیدس محاسباتی کرده بود.
 یادبود پیچ ارشمیدس در هلند
یادبود پیچ ارشمیدس در هلند
ارشمیدس از یافتههای ریاضیاتی خود برای درک بهتر مفاهیم بنیادیتر آن علم استفاده میکرد. بهعنوان مثال، او از مفهوم مقادیر بسیار کوچک در ریاضیات استفاده کرد و به درکی از محاسبات انتگرالی رسید. دستاورد او در آن بخش تا ۱۸۰۰ سال بعد منحصربهفرد بود.
اختراعها
پیچ ارشمیدس
داستانهای مختلفی دربارهی طراحی پیچ ارشمیدس وجود دارد که اکثر آنها حل مسئلهای کاربردی را دلیل تحقیقات دربارهی این موضوع میدانند. یکی از داستانها به مسئلهی پادشاه سیراکوزا اشاره میکند که بهدنبال راهی برای خالیکردن آب باران از بدنهی کشتیهایش بود. راهکار ارشمیدس آن بود که از لولهای خالی با ابزار مارپیچی استفاده کنند که با دسته در انتهای ماشین چرخانده میشود.
وقتی پایین لوله درون آبهای جمعشده قرار میگرفت و دستهی ماشین ارشمیدس میچرخید، آب به بالای لوله منتقل و تخلیه میشد. چنین راهکاری برای انتقال آب از دیگر منابع پاییندست در کاربردهایی همچون آبیاری هم مفید بود. در کشورهای درحالتوسعه، هنوز از پیچ ارشمیدس در آبیاری یا جابهجایی موادی همچون دانه و زغالسنگ استفاده میشود.
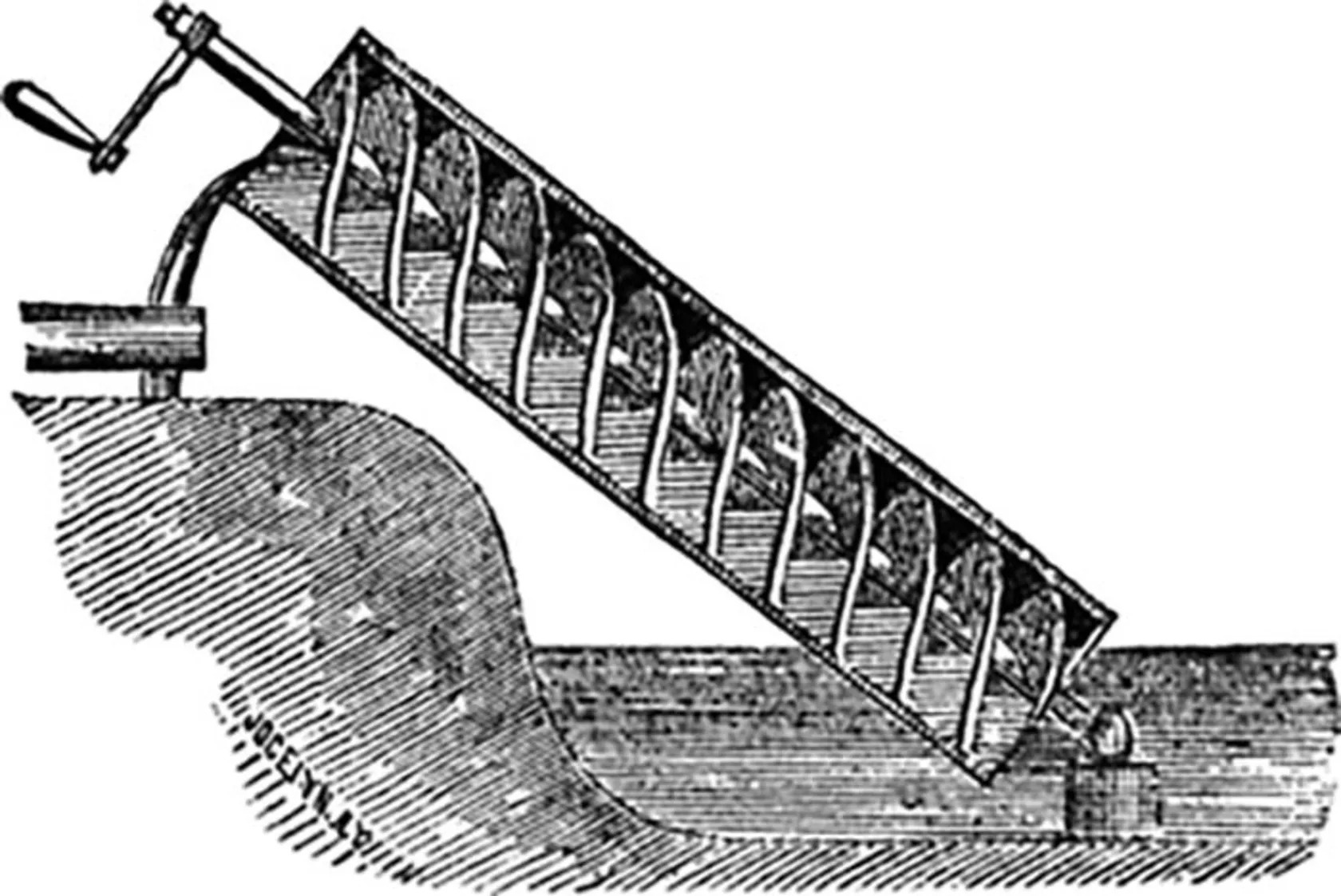 طرح شماتیک پیچ ارشمیدس
طرح شماتیک پیچ ارشمیدس
مورخان رومی اعتقاد داشتند اولین مفاهیم از مارپیچ ارشمیدس سالها قبل از آن در آبیاری باغهای معلق بابل بهکار گرفته شده بود. داستان تاریخی دیگر دربارهی مارپیچ آن است که اولینبار در سال ۱۸۳۹، کشتی بخار از موتور محرکی با آن ساختار استفاده کرد که بهاحترام مخترعش «اساس ارشمیدس» نامگذاری شد.
دست آهنین
همانطورکه گفته شد، ارشمیدس در ساخت تجهیزات نظامی برای شهر خود نیز فعالیتهایی کرد. او بازوی آهنینی طراحی کرد تا از سیراکوزا دربرابر کشتیهای مهاجمان دفاع کند. آنچه از این بازوی آهنین نقل میشود، بیشتر شبیه به فیلمهای علمیتخیلی قدیمی است. گویا طراحی آن بازو بهگونهای بوده که وارد کشتیها میشده و با بالاآوردن جلوِ آنها، موجب غرقشدن مهاجمان میشده است.
در دوران پس از ارشمیدس، تلاشهای زیادی شد تا نمونههایی از دست آهنین او برای بررسی کاربردیبودن طراحیهایش ساخته شود. در آخرین نمونه، در سال ۲۰۰۵ مستندی بهنام «اَبَرسلاحهای دوران باستان» پخش شد که در آن، نمونهای کاربردی از دست آهنین ارشمیدس ساخته شد.
 نقاشی دست آهنین ارشمیدس
نقاشی دست آهنین ارشمیدس
اشعههای گرمایی
برخی مورخان میگویند ارشمیدس احتمالا از آینههایی با ساختار سهموی برای سوزاندن کشتیهای مهاجمان به سیراکوزا استفاده میکرده است. در قرن دوم میلادی، اولین سند ادعا کرد در زمان سقوط سیراکوزا در سال ۲۱۲قم، کشتیهای مهاجمان به منطقه را ارشمیدس به آتش کشید. قرنها بعد نیز، آینههای آتشین بهعنوان ابزارهای ارشمیدس برای مقابله با کشتیهای دشمنان معرفی شدند.
روایتهای موجود از اشعههای گرمایی ارشمیدس ادعا میکنند آینهها برای متمرکزکردن اشعهی خورشید روی کشتیهای مهاجم استفاده میشد. امروزه، در وسایلی همچون خورپا (Heliostat) و کورههای خورشیدی از مفاهیم آن دستاورد ارشمیدس استفاده میشود.
دفاع از سیراکوزا یکی از انگیزههای اصلی اختراعهای ارشمیدس بود
در دورههای مختلف تاریخی، ادعاهایی مبنیبر خیالی و ساختگیبودن اسلحهی آینهای ارشمیدس مطرح شد. بهعنوان مثال، رنه دکارت آن را ادعایی دروغین میدانست؛ اما محققان دیگر میگفتند با استفاده از ابزارهای زمان ارشمیدس، مانند زرههای مسی نیز میشد چنان آینههایی طراحی کرد. در سال ۱۹۷۳، دانشمند یونانی آیونیس ساکاس تلاش کرد نمونهای کاربردی از اشعههای گرمایی ارشمیدس طراحی کند.
در آزمایش ساکاس، از آینهای مسی استفاده شد تا روند کار را دقیقا شبیه به شرایط ارشمیدس بررسی کنند. وقتی اشعههای خورشیدی با استفاده از آن آینهها به نمونهای ساختهشده شبیه کشتیهای رومی تابانده شد، کشتی نمونه در چند ثانیه آتش گرفت. البته، آن کشتی پوششی از قیر شبیه به کشتیهای دوران باستان داشت که احتمالا به شعلهورشدنش کمک کرد.
 نقاشی اشعههای گرمایی
نقاشی اشعههای گرمایی
علاوهبر آزمایش سال ۱۹۷۳، بررسیهای عملی دیگری نیز در سالهای بعد و حتی چند وقت اخیر روی احتمال کاربردیبودن طرح ارشمیدس انجام شد. آخرین نمونه به سال ۲۰۱۰ مربوط بود که گروهی از دانشمندان MIT در برنامهای بهنام MythBusters نمونهای از اسلحهی ارشمیدس را ساختند.
اختراعها و دستاورهای فیزیکی دیگر
اهرم اختراعی فیزیکی بود که پیش از ارشمیدس اختراع شد؛ منتها او برای اولینبار توانست توضیحی علمی و محاسباتی از نحوهی کار آن ابزار در رسالهاش با نام On the Equilibrium of Planes ارائه کند. او با بهرهگیری از همان یافتههای قبلی، توانست سیستم قرقرههای ترکیبی را برای استفاده در کشتیها اجرا کند که برای استفاده در کشتیها بسیار کاربردی شد.
در روایتهایی، بهبود عملکرد منجنیق نیز به ارشمیدس نسبت داده میشود که در جریان اولین جنگ کارتاژ انجام شد. نوآوری خارقالعادهی دیگر این دانشمند بزرگ اختراعی شبیه به کیلومترشمار بوده که با سیستمی چرخدندهای احتمالا پس از طی مسافت مشخص، گلولهای در جعبه انداخته و مسافت را محاسبه میکرده است.
سیسرو، یکی از مورخان مشهور دوران باستان، در یکی از روایتهایش، به مکانیزمی اشاره میکند که ارشمیدس برای توضیخ ساختار حرکتی کرهی زمین به دور خورشید و همچنین حرکتهای سیارههای دیگر استفاده میشده است. گفته میشود پس از اشغال سیراکوزا، این تجهیز را فرماندهای بهنام مارکوس کلادیوس مارسلوس به رُم برد.
یافتههای ریاضیاتی
تأثیراتی که ارشمیدس بر علم ریاضیات گذاشت، کمتر از تجربیات عملی و ساختههای فیزیکیاش نبودند. درواقع، آن دستاوردها نیز براساس همان یافتههای ریاضیاتی بهدست میآمدند.
یکی از روشهای محاسباتی مهم او در آن بخش، استفاده از مقادیر بسیار کوچک برای حل مسائل ریاضی بود که شباهت زیادی به محاسبات انتگرالی امروزی داشت.
از دیگر روشهایی که ارشمیدس بهکار میگرفت، مفهوم تعلیق به محال بود که درنهایت، بهحد مقبولی از پاسخ میرسید که محدودهی صحیحبودن آن نیز مشخص بود. این روش در ریاضیات بهنام «روش افنا» شناخته میشود که ارشمیدس در محاسبهی عدد پی از آن استفاده کرد.
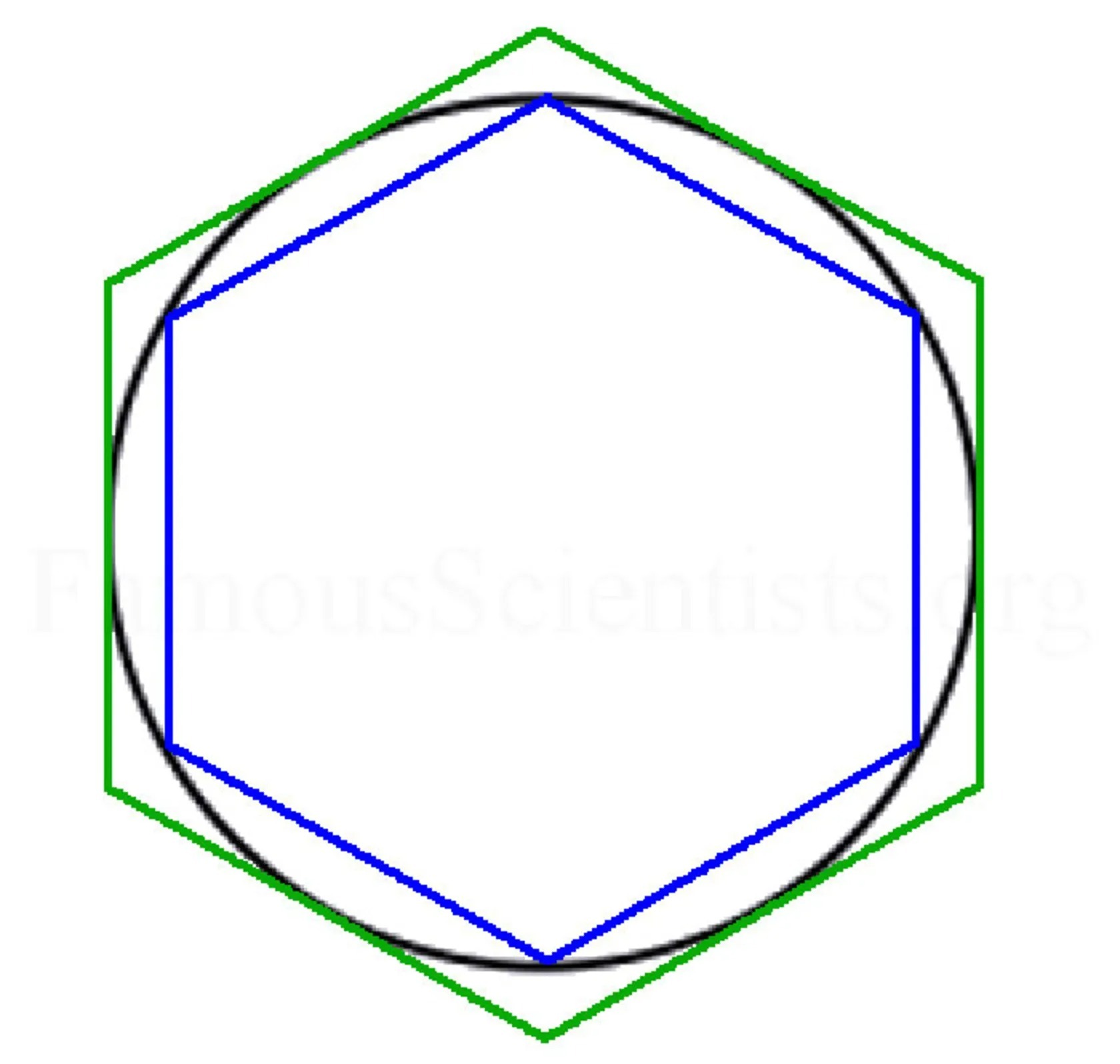 استفاده از ۶ ضلعی برای محاسبهی عدد پی
استفاده از ۶ ضلعی برای محاسبهی عدد پی
عدد پی ثابت مهمی در محاسبات اشکال منحنی است. ارشمیدس علاقهی بسیاری به کشف مشخصات ریاضیاتی سطوح منحنی همچون استوانه و مخروط و کُره داشت. او برای انجام آن محاسبات، ابتدا باید ثابت پی را کشف میکرد. امروزه، میدانیم عدد پی بهصورت ۳.۱۴۱۵۹ با دنبالهای نامنظم و نامتناهی از اعداد مشخص میشود. ارشمیدس که فرمول محاسبهی دایره، یعنی 2Πr را میدانست، برای محاسبهی عدد پی از روش افنا استفاده کرد.
روش افنا به دفعات در کشف مفاهیم ریاضی به ارشمیدس کمک کرد
ارشمیدس در شروع محاسباتش برای پیداکردن مقدار عدد پی، ابتدا ۲ مثلث را در خارج و داخل دایرهای با شعاع مشخص ترسیم کرد. او بهراحتی محیط مثلثها را محاسبه میکرد و میدانست محیط دایرهی مدنظر بین آن ۲ مقدار قرار میگیرد.
پس از محاسبهی نمونهی اول، از فرمول محاسبهی محیط چندضلعیها و در مرحلهی بعدی، از ۶ ضلعی برای محاسبهی حدودی استفاده شد. با افزایش تعداد ضلع چندضلعیها، محاسبات انجامشده به محیط دایره نزدیکتر میشد.
آزمایشهای ارشمیدس در روش افتا تا محاسبهی محیط ۹۶ ضلعیهای محاطی و محیطی دایره پیش رفت که شکل نهاییشان بسیار به دایره نزدیک بود. درنهایت، ارشمیدس به این نتیجه رسید که عدد Π بزرگتر از نسبت ۲۵۳۴۴/۸۰۶۹ و کوچکتر از ۲۹۳۷۶/۹۳۴۷ است.
میانگین محاسبات ارشمیدس عدد Π را ۳.۱۴۱۸۶ تا ۹ عدد اعشار نشان میدهد تنها ۱.۱۰۰۰۰ نسبت به عدد Π اثباتشده اختلاف دارد. درواقع، عدد Π که ارشمیدس کشف کرد تا دوران انقلاب دیجیتال، هنوز بهعنوان مرجع شناخته میشد. فراموش نکنید ارشمیدس از اندازهگیریهای ابزاری برای محاسباتش استفاده نکرد و هرآنچه بهدست آمد، محاسبات ذهنی فرمولها بود که بهدقت انجام شد.
 ۹۰ ضلعی محیطی و محاطی که به دایره نزدیک میشود
۹۰ ضلعی محیطی و محاطی که به دایره نزدیک میشود
محاسبهی حجم کُره؛ بزرگترین دستاورد ارشمیدس
ارشمیدس پس از کسب مهارت در محاسبات مرتبط با اشکال هندسی خطوط مستقیم، خود را برای مسئلهای بزرگتر آماده میکرد. او میخواست محاسبات سهبعدی را در اشکالی دشوار همچون کُرهها ادامه دهد. او بهعنوان اولین دانشمند تاریخ توانست حجم و سطح کُره را محاسبه کند.
پیش از ارشمیدس، اودوکسوس روش افنا را کشف کرده بود و ارشمیدس برای محاسبات سهبعدی از یافتههای اودوکسوس نیز استفاده کرد. همین محاسبات بود که او را برترین ریاضیدان دوران باستان میکند؛ محاسباتی که به انتگرال بهمعنای امروزی نزدیک بود.
روش ارشمیدس در محاسبات کُرهها در نوع خود واقعا شگفتانگیز بود. کُره برخلاف اشکالی همچون مکعب شکل منظمی ندارد. درواقع، مکعب تنها در لبهها تغییر شکل میدهد و کُره در هر بخش جزئیاش تغییر مسیر و شکل دارد.
ارشمیدس ابتدا برای محاسبهی مشخصات کره، آن را به ۲ نیمکره تقسیم کرد. اگر حجم یا مساحت هر نیمکره اندازهگیریکردنی بود، او میتوانست با دوبرابرکردن مقدار، به نتیجهی دلخواهش برسد.
پس از تقسیم کُره، ارشمیدس در ذهن خود آن را روی سطح صافی تصور و استوانهای در اطرافش ترسیم کرد. سطح مقطع استوانه برابر با دایرهی مرکزی کُره بود که روی زمین قرار داشت و ارتفاعش برابر با ارتفاع نیمکره بود. پس از آن مرحله، محاسبات ارشمیدس به انتگرال امروزی نزدیک شد. ارشمیدس تصور کرد برشهایی افقی از سطح استوانه ببُرد. برشها از بالای استوانه شروع میشود که در آن حالت، کُره در کوچکترین وضعیت خود قرار دارد. اگر به آن برش از بالا نگاه کنیم، سطح دایرهی ایجادشده تقریبا صفر خواهد بود.
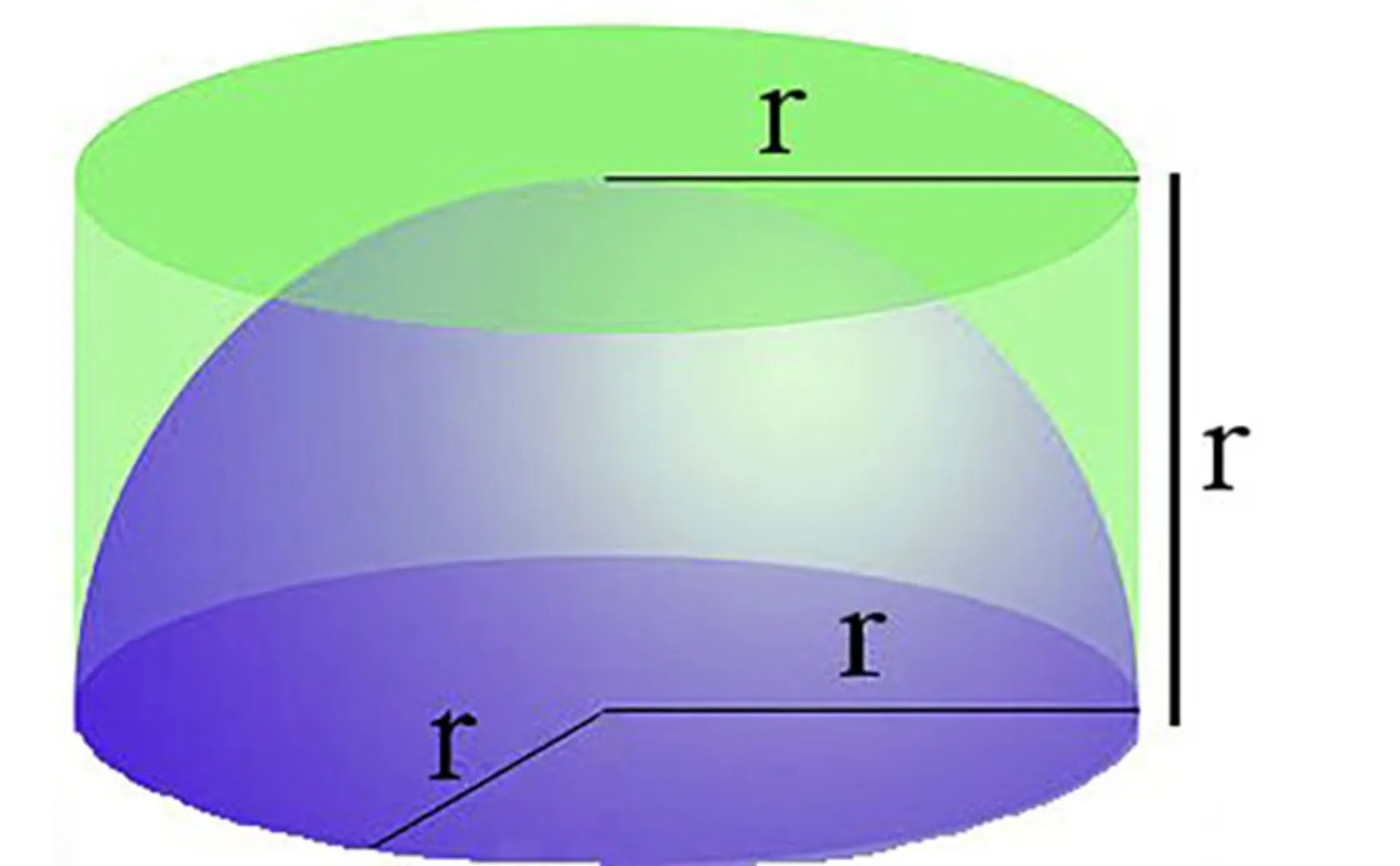 استفاده از استوانه و نیمکره برای محاسبهی حجم کره
استفاده از استوانه و نیمکره برای محاسبهی حجم کره
روند برش استوانه با نیمکرهی داخل آن، در محاسات ذهنی ارشمیدس بهمرور پیش رفت و با پایینآمدن از ارتفاع استوانه، دایرهی داخلی نیز بزرگتر میشد.هدف محاسبات کشف مقادیری بود که در بین دایرهی داخلی (نشاندهندهی سطح مقطع کُره) و دایرهی خارجی ثابت (نشاندهندهی سطح مقطع استوانه) بهدست میآمد.
درنهایت، ارشمیدس مناطق محاسبهشده را در ارتفاع هر برش ضرب کرد تا حجم اشغالشده از هرکدام را پیدا کند. ارتفاع هر برش بسته به تصورات ذهنی او بود. مجموع این محاسبهها حجم موجود بین نیمکره و استوانه را نشان داد. اگر ارشمیدس همان مسیر بالا را با بینهایت کوچککردن برشها ادامه میداد، دقیقا روش انتگرالی بهکار گرفته میشد که ۱۸۰۰ سال بعد نیوتن کشف کرد.
ارشمیدس درادامهی محاسبات به مخروطی رسید که حجمش با مجموع حجم اشغالشدهی برشها برابر بود. دایرهی پایینی آن مخروط برابر با سطح مقطع استوانه و ارتفاعی هم با استوانه برابر میشد. درنهایت، حجم نیمکره با حجم استوانه منهای حجم مخروط مدنظر برابر بود. ازآنجاکه حجم استوانه و مخروط اندازهگیریکردنی بود، حجم کُره درنهایت با فرمول V = 4⁄3πr3 اندازهگیری شد.
عدد فوقبزرگ
یکی از دستاوردهای مهم ارشمیدس در ریاضیات محاسبهی عددی فوقبزرگ بود که بهنام عدد هیولایی (Beat Number) هم شناخته شد. روایت آن دستاورد به داستانی میرسد که مردم به ارشمیدس گفتند نمیتواند تعداد ماسههای موجود در ساحل را محاسبه کند. ارشمیدس در پاسخ به این ادعای غیرمنطقی، عددی فوقبزرگ طراحی کرد و با استفاده از آن، نهتنها دانههای ماسهی موجود در صحرا، بلکه تمام جهان را محاسبه کرد.
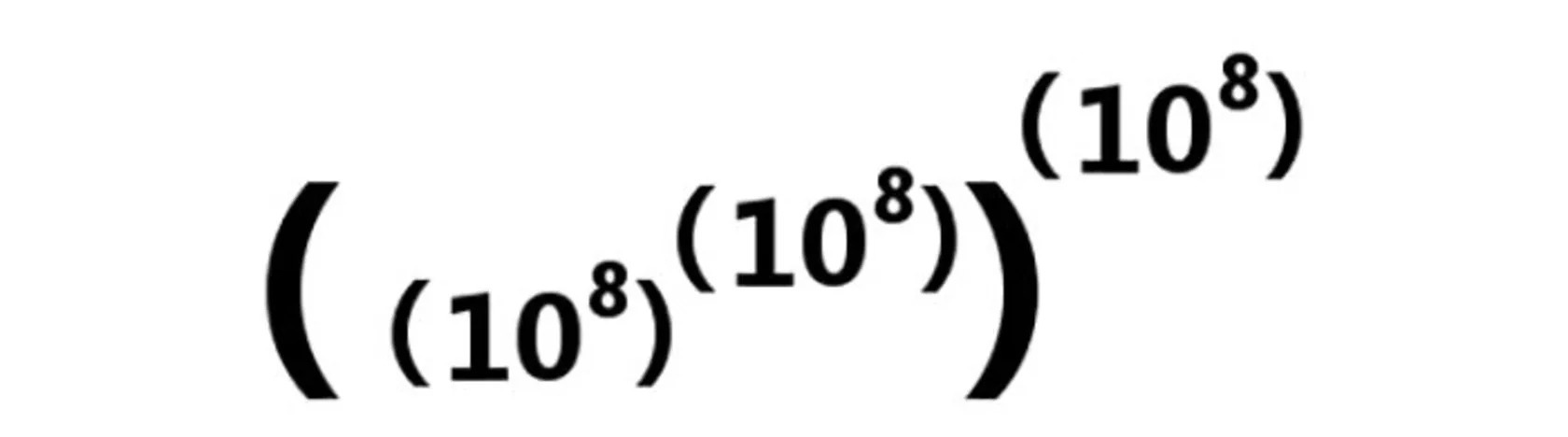
اولین مسئلهای که ارشمیدس در محاسبات خود با آن روبهرو شد، سیستم اعداد یونانی بود که برای هر عدد، یک حرف در نظر میگرفت. درنتیجه، اعداد بسیار بزرگ مشکل ایجاد میکردند؛ چون حروف کافی برای نمایش آنها در الفبا وجود نداشت. تا آن زمان، بزرگترین عدد علوم یونانی ۱۰۰۰ بود.
ارشمیدس در کتابش با نام The Sand Reckoner، ایدهی ناممکنبودن محاسبهی تعداد ماسهها را بهمبارزه طلبید. درواقع، او محاسبهای انجام نداد؛ اما اعدادی معرفی کرد که میتوانند حتی از تعداد ماسههای موجود در کل جهان هم بیشتر باشند. محاسبات او برپایهی مفاهیمی بود که امروزه با نام «توان» میشناسیم. محاسبات ارشمیدس برای تعریف عدد مدنظرش، از حوصلهی این مقاله خارج است و تنها لازم است بدانید او به عددی برابر با تصویر بالا رسید که عدد یک با ۸۰ کوادریلیون صفر میشود.
مساحت زیر نمودار سهمی
هرچهبیشتر تحقیقات ارشمیدس را مطالعه میکنیم، این تصور دشوارتر میشود که او در سالهای قبل از میلاد مسیح به چنین دستاوردهایی رسیده است. دانشمند بزرگ یونانی در فکر محاسبهی مساحت زیر نمودار سهمی نیز بود. او برای رسیدن به مقصودش، از مفاهیم سریهای هندسی استفاده کرد.
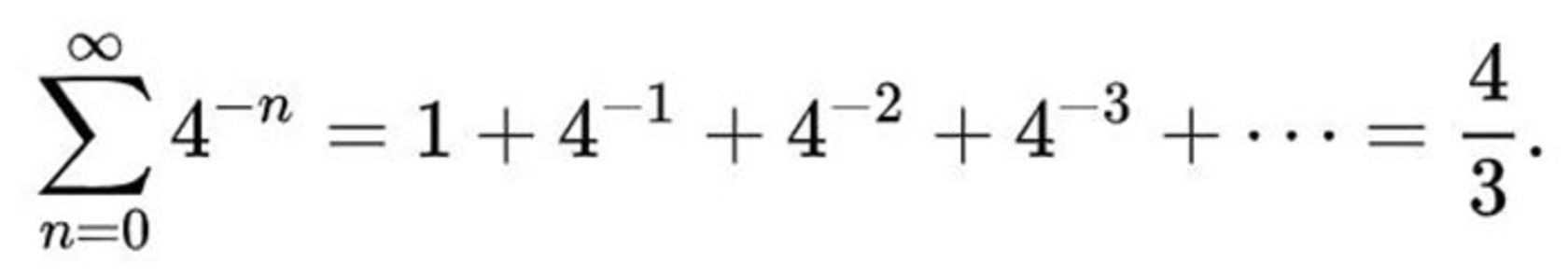 سری هندسی ارشمیدس برای محاسبهی سطح زیر نمودار سهمی
سری هندسی ارشمیدس برای محاسبهی سطح زیر نمودار سهمی
ارشمیدس پس از محاسبههای متعدد، به این نتیجه رسید مساحت بین یک سهمی و یک خط مستقیم، ۴.۳ برابر مثلث محاط بهشکلی است که در تصویر زیر میبینید. او راهحل مسئله را بهصورت سری متناهی هندسی با فرمول بالا بیان کرد.
داستان علمیتخیلی تاج پادشاه
اکثر ما ارشمیدس را با داستان معروف «یافتم، یافتم» و حمامکردن او میشناسیم. شاید صحیحبودن بخشهایی از این داستان مبهم باشد، اما توضیحی بر یکی از یافتههای باارزش آن دانشمند بزرگ محسوب میشود. پادشاه سیراکوزا، یعنی هیرو دوم، به آهنگری مقداری طلا داد و دستور داد تاجی برای او بسازد.
تاجی که ساخته شد، وزنی برابر با طلاهای پادشاه داشت؛ اما هیرو کمی مشکوک شد. پادشاه شک داشت آهنگر مقداری از طلاها را دزدیده و از نقره بهجای آنها استفاده کرده است. او نمیتوانست ادعایش را ثابت کند؛ بههمیندلیل، از ارشمیدس کمک خواست.
 پرترهی داستان کشف قبر ارشمیدس
پرترهی داستان کشف قبر ارشمیدس
در آن زمان، مفهوم چگالی تاحدودی درک شده بود و ارشمیدس میدانست وزن طلا در ابعادی برابر با نقره بیشتر است. مشکل اصلی شکل نامنظم تاج بود؛ در نتیجه، وزن آن مشخص و حجمش اندازهگیرینشدنی میشد. روایتها میگویند ارشمیدس با مقایسهی حجم آبی که از انداختن دو قطعهی متفاوت طلا و نقره جابهجا میشود، توانست حجم مدنظر را محاسبه کند.
داستان حمام و کشف مفهوم چگالی احتمالا افسانهای بیش نیست
با توجه به محاسبههای ارشمیدس، اگر وزن تاج را یک کیلوگرم و وزن طلای دادهشده به آهنگر را نیز یک کیلوگرم در نظر بگیریم، باید انداختن هر دو قطعه (تاج و طلایی یک کیلوگرمی) در مقدار مساوی آب، حجمی مساوی از آن را بالا میآورد. ارشمیدس با این آزمایش بهنتیجه رسید که تاج ساختهشده ترکیبهایی از نقره هم دارد. این یافته هم برای پادشاه و هم آهنگر عواقب ناخوشایندی داشت.
داستان معروف دربارهی این یافته میگوید ارشمیدس هنگام حمامکردن و واردشدن در وان آب، متوجه بالاوپایینشدن سطح آن شد. درک آن مفهوم آنقدر او را خوشحال کرد که طبق داستان، به کوچه دوید و فریاد «اورکا، اورکا» بهمعنای «یافتم، یافتم» سر داد.
کتابها و مقالهها
نوشتههای ارشمیدس به زبان یونانی باستان دوریک (Dorik) بود. برخلاف اقلیدس، دستاوردهای نوشتاری ارشمیدس بهخوبی حفظ نشدند و فقط ۷ عدد از رسالهها براثر ارجاعدادن دیگر دانشمندان به آنها زنده ماندند. ارشمیدس در زمان حیات، ازطریق ارتباط و مکاتبه با ریاضیدانان اسکندریه یافتههای علمیاش را نشر میداد.
در قرن پنجم میلادی، اولین اقدام جدی برای جمعآوری آثار ارشمیدس انجام شد و تألیف بعدی نیز در قرن پانزدهم بهاتمام رسید. ازجمله دانشمندان مشهوری که به یافتههای ارشمیدس ارجاع دادند، گالیله بود که در سال ۱۵۸۶، مفهوم تعادل هیدرواستاتیکی را با الهام از ارشمیدس توضیح داد.
این رساله، در ۲ جلد و شامل توضیحاتی دربارهی قوانین اهرمها نوشته شد. ارشمیدس نیروهای موجود در سیستم اهرمها را در این رساله توضیح داد و نسبت وزن و فاصلهی مؤلفههای حاضر در آن را بررسی کرد. در بخشهای دیگری از رساله، محاسبات او برای یافتن مرکز ثقل و مساحت اشکال محتلف هندسی بیان شده است.
On the Measurement of Circles و On Spirals
این رسالهها بهصورت مکاتباتی بین ارشمیدس و دانشمندی در اسکندریه نوشته شدهاند. موضوع اصلی همانطورکه از نام مقالهی اول برمیآید، به محاسبهی عدد پی مرتبط است و آن را مقداری بین کسرهای ۲۲۳.۷۱ و ۲۲.۷ بیان میکند.
در رسالهی دوم، به مارپیچ ارشمیدس اشاره شده که بهنوعی جزو اولین تعاریف از منحنیهای مکانیکی محسوب میشود. رسالهی دیگری که در توضیح مساحت اشغالشدهی سهمی و خط مستقیم ارائه شد، The Quadrature of the Parabola نام داشت.

پازل Ostomachion On the Sphere and the Cylinder
مهمترین دستاورد نظری ارشمیدس در رسالهی او دربارهی کُره و استوانه شرح داده شد. در این مقاله، ارشمیدس به یافتههایش دربارهی ارتباط کُره با استوانهی محیطی اشاره میکند. فرمولهایی که در بخشهای پیشین برای محاسبهی حجم و سطح استوانه و کُره توضیح دادیم، در این رساله مطرح شدهاند. ارشمیدس در رسالهی مشابه دیگر بهنام On Conoids and Spheroids روشهای محاسبهی حجم و سطح انواع مخروط و سطح مقطع را توضیح میدهد.
On Floating Bodies
یکی از دستاوردهای مهم دیگر ارشمیدس که کمتر به آن پرداختیم، مطالعات سیالاتی او بود. او قوانین تعادل مایعات را در رسالهی مذکور توضیح داد. او ادعا کرد آب بهعنوان شناختهشدهترین مایع پیرامون یک مرکز ثقل، شکلی کُروی بهخود میگیرد.
Ostomachion
یکی از رسالههای جذاب دانشمند یونانی در علم هندسه، همین رساله است که بهنام جعبهی ارشمیدس نیز شناخته میشود. این مقاله مسئلهای شبیه به پازلهای تنگرام را شرح میدهد که نسخهی کاملتر آن در کتاب گمشدهی ارشمیدس (Palimpsest) یافت شد. این دانشمند بزرگ یونان باستان در مقالهاش، مساحت ۱۴ شکل را محاسبه میکند که درکنارهم دایرهای شکل میدهند.
در سال ۲۰۰۳ در دانشگاه استنفورد، رویل نتز تحقیقاتی انجام داد که مقالهای ارزشمند بهدنبال داشت. نتز در مقالهاش دربارهی رسالهی ارشمیدس توضیح داد هدف ارشمیدس پیداکردن راههای مختلف برای شکلدادن مربع با استفاده از آن اشکال بوده است. او در پایان گفت ۱۷،۵۱۲ روش برای ساختن مربع با اشکال مدنظر وجود دارد. ریاضیدانان این پازل ارشمیدس را پایهای برای درک مفاهیم ترکیبیات میدانند.
 طرحی از داستان مرگ ارشمیدس
طرحی از داستان مرگ ارشمیدس
مرگ اسطورهای و یادگارهای جاودان ارشمیدس
ارشمیدس شخصیتی درخوراحترام در سیراکوزا بود. او به حفظ شهر دربرابر حملهی رومیها کمک شایانی کرده بود و ۲ سال نیروهای آنها را بهعقب راند. حملات ارتش روم به سیراکوزا متوقف نمیشد و درنهایت، در سال ۲۱۲قم، نیروهای مارسلوس شهر را دراختیار گرفتند. مارسلوس احترام زیادی برای ارشمیدس قائل بود و سربازانش را برای دستگیری زندهی او مأمور کرد.
مرگ ارشمیدس نیز با داستان شهر محل تولدش گره خورد
داستان مرگ ارشمیدس میگوید ظاهرا او از اشغال شهر آگاه نبوده و درگیر محاسبات ریاضیاتیاش بوده است. وقتی سرباز رومی از او میخواهد همراهش به نزد مارسلوس برود، ارشمیدس درخواستش را رد میکند و به مطالعهاش ادامه میدهد. سرباز رومی نیز با عصبانیت به این دانشمند بزرگ حمله میکند و او را در ۷۵ سالگی میکشد.
مارسلوس که از مرگ ارشمیدس بسیار ناراحت و عصبانی شد، دستور داد او را با احترام و تشریفات کامل بهخاک بسپارند. روی قبر ارشمیدس همانگونه که خودش وصیت کرده بود، شکلی از کُره و استوانه حک شد.
گالیله یکی از دانشمندانی بود که قرنها بعد، در بسیاری از اکتشافات خود از ارشمیدس به نیکی یاد میکرد. او ارشمیدس را اَبَرانسان میدانست. دانشمند بزرگ دیگر، لایبنیتس، دربارهی او گفت:

یکی از چالههای ماه بهنام ارشمیدس نامگذاری شد. بهعلاوه، یکی از رشتهکوههای موجود در آن کُره نیز بهنام این دانشمند بزرگ یونانی است. جایزهی بزرگ ریاضیات با نام مدال فیلدز، منقش به تصویری از ارشمیدس است که درکنار آن، نقشی از کُره و استوانه نیز حک شده است. کشورهای مختلف جهان از آلمانشرقی و یونان و ایتالیا تا نیکاراگوئه و سانمارینو و اسپانیا، تمبرهای یادبودی به افتخار این دانشمند بزرگ چاپ کردهاند.
علاوهبر آنچه گفته شد، فهرست بلندبالایی در ویکیپدیا موجود است که تمامی موارد نامگذاریشده به افتخار ارشمیدس را شرح میدهد. از میان آنها، میتوان انواع مفاهیم فیزیکی، ریاضیاتی، فناوری، سختافزارها و نرمافزارهای کامپیوتری، نامهای نجومی و موارد دیگر را مثال زد. قسم ارشمیدس یکی از آن مواردی است که برخی مهندسان پیش از شروع فعالیت کاری آن را یاد میکنند.
منبع: عصر ایران



























