«ریاضیات» چقدر شبیه «دین» است؟

ریاضیات و دین هر دو مظهر حقایق ابدی و شگفتانگیز هستند. هردوی آنها احساساتی مشابه را در دنبالکنندگانشان برمیانگیزند که شاید بشود آن را حاصل نوعی «تماس» با جاودانگی توصیف کرد.
فرادید| در نگاه نخست، شاید به نظر برسد که ریاضیات و دین اشتراکات کمی با هم دارند، با این حال هر دوی آنها احساسات مشابهی را بین طرفداران خود برمیانگیزند. درک کامل و جامع هر دو حوزه مستلزم سالها مطالعه شدید هستند و انگار درک حقیقتی گریزان و ابدی سبب ایجاد احساس هیبت و شادی میشود، خواه این درک در حوزه ریاضی باشد و خواه در الهیات.
به گزارش فرادید، آلبرت اینشتین در ادای احترام چشمگیری به اِمی نوتر ریاضیدان پس از مرگ او در سال ۱۹۳۵، یک متن قدردانی در نیویورک تایمز نوشت و اکتشافات او را ستود و در عین حال درسهای بزرگتری از زندگی درباره کوشش متواضعانهی متفکرانی مانند او که روشنگر درک بشر هستند، ترسیم کرد. اینشتین گفته است ریاضیات، سرودن شاعرانۀ ایدههای منطقی است. او با اشاره به موفقیت نوتر توضیح میدهد: «در این تلاش برای رسیدن به زیبایی منطقی، فرمولهای معنوی لازم برای نفوذ عمیقتر به قوانین طبیعت کشف میشوند.»
واژهی «معنوی» یک صفت شگفتانگیز برای «فرمولها» است؛ اینطور نیست؟ شاید واژه Elegant (به معنای شیک، برازنده) انتخاب مرسومتری باشد، اما اینشتین واژگان خاص خود را برای تأکید بر سطح عمیقتری از زیبایی ریاضی انتخاب کرد.
زبان دینی معمولاً توسط ریاضیدانان به کار گرفته میشود، حتی میان کسانی که دیندار نیستند. حتی پل اردوس، ریاضیدان پرکار مشهوری که علاقه داشت خدا را به عنوان فاشیست عالی معرفی کند نیز دوست داشت از «کتاب خداوند» که در آن تمام زیباترین شواهد ثبت شده است، صحبت کند. اردوس یک بار به طعنه گفت: «مجبور نیستید به خدا ایمان داشته باشید، اما باید به «کتاب» ایمان داشته باشید.» مقصود او از کتاب، اشارهی آشکاری به جاودانگی ایدههای ریاضی بود که وجود و تداوم آنها با طبیعت ابدی برابر است؛ همان چیزی که الهیات بیش از هر حوزۀ دیگری از آن صحبت میکند.
ریاضی چقدر شبیه دین است؟
مشغلههای ریاضیات و دین از بسیاری جهات شبیه هم هستند و احساسات و واکنشهای مشابهی را در طرفداران خود برمیانگیزند. با این حال، این مشاهده یک ادعای جهانی در مورد عقاید دینی متفکران ریاضی نیست. در طول تاریخ ریاضی، پیروان بسیاری از سنتهای دینی مختلف وجود داشتند، رامانوجان، اگنسی، اویلر، خوارزمی یا حتی فیثاغورثیها. با این حال، بسیاری از ریاضیدانان بیخدا یا آگنوستیک هم وجود داشتهاند. یک نظرسنجی در سال ۱۹۹۸ از اعضای آکادمی ملی نشان داد ریاضیدانان آن سازمان نسبت به عموم مردم کمتر مذهبی هستند (اگرچه اندکی مذهبیتر از سایر دانشمندان هستند). با این حال، کسانی که به دنبال تجربیات ریاضی هستند و کسانی که به دنبال تجربیات مذهبی هستند، اشتراکات زیادی دارند.
چنین اشتراکی تا حدی به دلیل قدرت توضیحی ریاضیات و دین است. ریاضیات بینشهایی در مورد پدیدههای فیزیکی و دین بینشهایی در مورد طبیعت انسان ارائه میدهد. از این رو، طبیعی است آنها را در حوزههای مربوطهشان مقایسه کنیم. حقایق آنها همیشه آشکار نیست و کشف آنها گاهی اوقات مستلزم سالها مطالعه است و گاهی اوقات تفاسیر یا کاربردهای آنها را باید به چالش کشید.
تلاش و کوشش در هر دو حوزه به پاداش منتهی میشود؛ پاداشی که عبارت است از بینشهای نافذ. سالها مطالعه در حوزهی ریاضیات به فرد امکان میدهد ساختارهای پنهان جهان را به گونهای تجسم کند که به طبیعت ثانی تبدیل شود. به همین ترتیب، سالها عبادت پرهیزکارانه، بینش اخلاقی سالم به همراه دارد، طوری که وقتی آن بینش با فطرت خودخواهانه فرد در تضاد قرار گیرد، فرد هیچ تردیدی در انجام کار درست ندارد. در چنین رشدی، شادی و پاداش وجود دارد.
افزون بر این، هر دو حوزه امکان غافلگیری را فراهم میکنند: لحظات شادیآوری که در آنها تغییر جهتگیری فوری و حل شدن ناگهانی و اعجابانگیز مشکلات سخت را تجربه میکنید. برای مثال، یک پرسش مهم در بسیاری از ادیان این است که شخص چگونه گناهانش را جبران میکند. امکان غیرمنتظره بخشش در کفاره گناه، راهحل چشمگیری است که بیشباهت به راهحل غیرمنتظرهی یک مسئله دشوار ریاضی نیست. چنین لحظاتی در هر دو حوزه شایسته شکرگذاری (هالِلویا) هستند.
این ریتم مدیتیشن که با امکان غافلگیری شادیآور مشخص میشود به این معناست که هم تجربیات ریاضی و هم تجربیات مذهبی میتوانند مکانهایی برای پناه و امید باشند. در طول همهگیری کووید، فروش پازلها افزایش یافت. چرا؟ چون در مواقع پریشانی شدید، مردم به دنبال چیزی هستند که حواسشان را پرت کند و درگیر شدن در پازلها شکل لذتبخشی از تفکر ریاضی است که فقط به ریاضیدانان محدود نمیشود. حل پازل موجب شادی میشود و تجربه درگیری با پازل به ما آموزش میدهد با هر معمای جدید به یافتن پاسخ امیدوار باشیم. فرد دیندار به جای پازل به دعا روی میآورد. بنابراین، تعمق در حل یک معما یا دعا خواندن در انتظار امیدوارانه برای نتیجه یا راهحل تفاوت زیادی ندارند.
ریاضیات و فناناپذیری
هم در ریاضیات و هم در بیشتر ادیان، شخص با واقعیت اشیای فناناپذیری روبرو میشود که قابلرویت نیستند. افراد مذهبی معمولاً به دلیل اعتقاد به خدای ماوراء طبیعی غیر فیزیکی و تعامل با او از سوی ملحدان تمسخر میشوند. با این حال، همین مسخرهکنندگان همگی یاد گرفتهاند که با مفاهیم غیرفیزیکی افلاطونیِ اعداد کامل، بشمارند، ارتباط برقرار کنند و استدلال کنند و حتی آنها را در آنچه که ما «جهان واقعی» مینامیم، به کار گیرند.
همانطور که مورخ ریاضیات، دی. ای. اسمیت زمانی اشاره کرد، ریاضیات ما را «در قالب قوانین ابدی ریاضی با جاودانگی در تماس قرار میدهد». افزون بر این، بسیاری از دانشمندان حتی از چگونگی این تعامل شگفتزده شدهاند. خود اینشتین میپرسد: «چطور ممکن است ریاضیات که در نهایت محصول تفکر بشری مستقل از تجربه است، به طرز تحسینآمیزی با موضوعات واقعی مناسب باشد؟» به بیان دیگر، این موضوع باید ما را شگفتزده کند که موضوعات ریاضی افلاطونی با دنیای واقعی تعامل سازنده دارند - اما این شگفتی برای ما عادی شده است.
در هر دو حوزه ریاضیات و دین، شخص حقایق را با چنان عمق متعالی درک میکند که هیبت و احترام را برمیانگیزد. کرامت انسانها، فاسد بودن ماهیت گناه، اهمیت عدالت و قدرت بخشش، همگی حقایقی هستند که در یک تجربه دینی عمیقاً احساس میشوند. به طور مشابه، مواجهات فرد با زیبایی تقارن یا ارتباط عمیق بین ایدههای متفاوت در ریاضیات میتواند شگفتی عمیقی را در تجربیات ریاضی برانگیزد. گاهی اوقات این قبیل مواجهات فقط اجمالی هستند؛ اشارهای گذرا به اینکه چیزی وجود دارد که هم بزرگتر و هم نامرئی است.
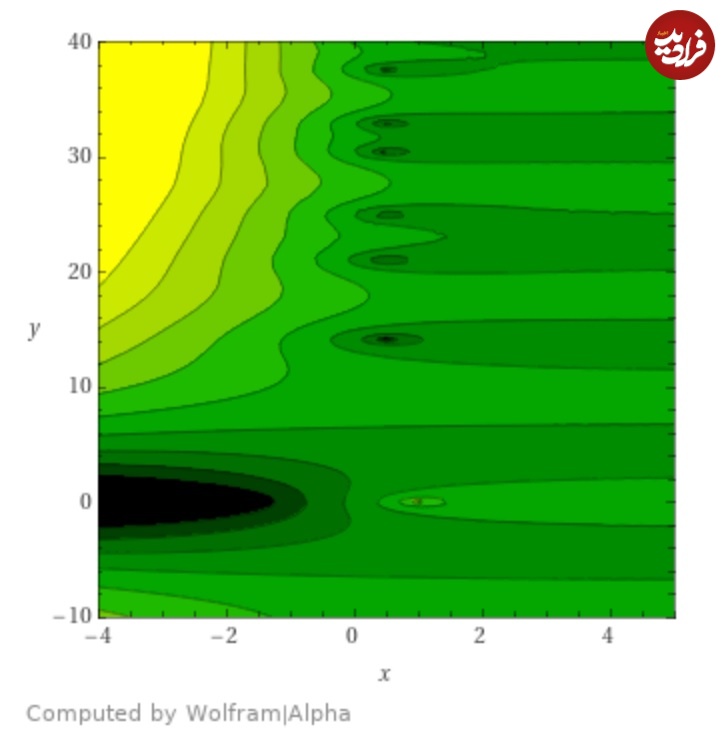
چند صفر از تابع زتا ریمان به صورت نقاط تاریک در امتداد خط عمودی x=½
ریاضیدانی که مشاهده میکند مقادیر ویژهی ماتریسهای تصادفی، شباهت قابلتوجهی با صفرهای تابع زتای ریمان دارند، به این پرسش سوق داده میشود: آیا این ارتباط زیبا تصادفی است یا سرنخی وسوسهانگیز است که به واقعیتی عمیقتر اشاره دارد؟ به طور مشابه، یک دیندار وفادار ممکن است دست خدا را در رویدادهای انسانی ببیند که دیگران آن را تصادف میپندارند؛ اما فرد دیندار حین رویارویی با امر الهی، خود را موظف به عبادت میداند. اینشتین نیز چنین احساسی را بیان میکرد: «اگر چیزی در من باشد که بتوان آن را مذهبی نامید، پس تحسین بیحد و حصر برای ساختار جهان است، تا آنجا که علم ما بتواند آن را آشکار کند.» بنابراین به یک معنا دانشمندان با عبادت بیگانه نیستند.
این اشتراکات تجربی میان رشتههای ریاضی و دینی میتواند پلی برای تفاهم ایجاد کند، خواه علایق شما به اعداد باشد، خواه به چیزهای باطنی و خواه هیچ کدام. حتی اگر هیچ ارتباط عاطفی با هیچ فرمول ریاضی یا هیچ تعلیم دینی نداشته باشید، باز هم ممکن است شروع کنید به درک اینکه چرا دیگران چنین ارتباطات عاطفی را با علایقشان تجربه میکنند. یک فرمول قدرت توضیحی دارد و نشاندهندهی یک بینش نافذ است؛ مثل اوج گرفتن پس از یک مبارزه سخت و امید به درک چیزی عمیق. نمونه توانایی انسانها در تعامل با حقایق نامرئی و انتزاعی است که بر دنیای ما اثر میگذارند. اگر مانند اینشتین اهمیت متعالی فرمولهای امی نوتر را برای پیشرفت انسان و درک قوانین طبیعت درک کنیم، پس در واقع: اشتباه نیست اگر چنین بینشهایی را معنوی بنامیم.
مترجم: زهرا ذوالقدر
























